GAT GENERAL TEST Sample 3 Questions Solution(Quantitative)
GAT GENERAL TEST Sample 3 Questions Solution(Quantitative)
Quick Response Question
- 350 x 1 = 0 + 350 = 350
- 233 + 0 = 1 x 233 = 233
- 20 + ( 25 + 44) = (20 + 25 ) + 44
- 21 x (9 + 11) = (21 x 9 ) + (21 x 11)
- 250 x (10 + 1) = (250 x 10) + ( 250 x 1)
GCD HCF LCM
Answer Q1:
The solution of this question can be calculated using both HCF and GCD.GCD Method
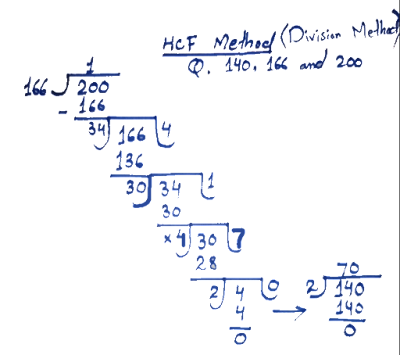
To find the greatest length of pieces that can be obtained when cutting three strings of lengths 140 cm, 166 cm, and 200 cm into equal-sized pieces without any string left over, we need to find the greatest common divisor (GCD) of these three lengths.
To find the greatest length of pieces that can be obtained when cutting three strings of lengths 140 cm, 166 cm, and 200 cm into equal-sized pieces without any string left over, we need to find the greatest common divisor (GCD) of these three lengths.
Using the prime factorization method, let's find the GCD:
Step 1: Prime factorize the numbers 140, 166, and 200.
- 140 = 2^2 * 5 * 7
- 166 = 2 * 83
- 200 = 2^3 * 5^2
Step 2: Identify the common prime factors among the three numbers and their respective minimum powers.
The common prime factors are 2 and 5.
The minimum powers of 2 are 2^1 = 2.
The minimum powers of 5 are 5^0 = 1.
Step 3: Multiply the minimum powers of the common prime factors.
2 * 5^0 = 2.
Therefore, the greatest common divisor (GCD) of 140 cm, 166 cm, and 200 cm is 2 cm.
Hence, the greatest length of pieces that can be obtained without any string left over is 2 cm.
HCF Method (Division Method)
HCF Method (Prime Factorization Method)
To find the greatest length of pieces that can be obtained when cutting three strings of lengths 140 cm, 166 cm, and 200 cm into equal-sized pieces without any string left over using the Highest Common Factor (HCF), we can directly calculate the HCF of these three lengths.
Step 1: List the factors of each length:
Factors of 140 cm: 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
Factors of 166 cm: 1, 2, 83, 166
Factors of 200 cm: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200
Step 2: Identify the common factors among the three numbers:
Common factors: 1 and 2.
Step 3: Determine the highest common factor (HCF) by selecting the greatest common factor from the common factors:
HCF = 2 cm.
Therefore, the greatest length of pieces that can be obtained without any string left over is 2 cm.
Answer Q2:
Let's find the greatest sum of money that is exactly contained in Rs. 165, Rs. 255, and Rs. 345 using the Highest Common Factor (HCF) method.
Step 1: List the prime factors of each amount:
Rs. 165 = 3 * 5 * 11
Rs. 255 = 3 * 5 * 17
Rs. 345 = 3 * 5 * 23
Step 2: Identify the common prime factors among the three amounts:
Common prime factors: 3 and 5.
Step 3: Determine the highest common factor (HCF) by selecting the product of the common prime factors:
HCF = 3 * 5 = 15.
Therefore, the greatest sum of money that is exactly contained in Rs. 165, Rs. 255, and Rs. 345 is Rs. 15.
Answer Q3:
To find the least number of biscuits that can be equally divided among 9, 12, and 18 children, we need to find the least common multiple (LCM) of these three numbers.
Step 1: List the multiples of each number:
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, ...
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, ...
Multiples of 18: 18, 36, 54, 72, 90, 108, 126, ...
Step 2: Identify the common multiples among the three numbers:
Common multiples: 36, 72, 108, ...
Step 3: Determine the least common multiple (LCM) by selecting the smallest common multiple from the common multiples:
LCM = 36.
Therefore, the least number of biscuits that can be equally divided among 9, 12, and 18 children is 36 biscuits. Each child will receive 4 biscuits (36 biscuits divided equally among 9, 12, and 18 children).
Answer Q4:
To find the greatest length of pieces that can be obtained when cutting three strings of lengths 75 cm, 100 cm, and 150 cm into equal-sized pieces without any string left over, we need to find the greatest common divisor (GCD) of these three lengths.
Using the prime factorization method, let's find the GCD:
Step 1: Prime factorize the numbers 75, 100, and 150.
- 75 = 3 * 5 * 5
- 100 = 2 * 2 * 5 * 5
- 150 = 2 * 3 * 5 * 5
Step 2: Identify the common prime factors among the three numbers and their respective minimum powers.
The common prime factors are 5.
The minimum powers of 5 are 5^2 = 25.
Therefore, the greatest common divisor (GCD) of 75 cm, 100 cm, and 150 cm is 25 cm.
Hence, the greatest length of pieces that can be obtained without any string left over is 25 cm.
HCF Method (Division Method)
HCF of 12 and 15 using the Prime Factorization Method
Answer Q5:
To find when the first bell of the junior section (45 minutes) and the senior section (1 hour or 60 minutes) will ring together again, we need to find the least common multiple (LCM) of these two durations.
Step 1: Convert 1 hour to minutes.
1 hour = 60 minutes.
Step 2: List the multiples of each duration:
Multiples of 45 minutes: 45, 90, 135, 180, 225, 270, ...
Multiples of 60 minutes: 60, 120, 180, 240, 300, 360, ...
Step 3: Identify the common multiples among the two durations:
Common multiples: 180, 360, ...
Step 4: Determine the least common multiple (LCM) by selecting the smallest common multiple from the common multiples:
LCM = 180 minutes.
Now, let's calculate the time when the two bells will ring together again:
The first bell for each section rings at 8:00 am. Adding 180 minutes to this time:
8:00 am + 3 hours (180 minutes) = 11:00 am.
Answer Q6:
Therefore, the first bell of the junior section and the senior section will ring together again at 11:00 am.
To find when the periods for primary classes (30 minutes) and other classes (35 minutes) will start together, we need to find the least common multiple (LCM) of these two durations.
Step 1: Find the LCM of 30 minutes and 35 minutes.
To do this, let's list the multiples of each duration:
Multiples of 30 minutes: 30, 60, 90, 120, 150, 180, 210, 240, ...
Multiples of 35 minutes: 35, 70, 105, 140, 175, 210, 245, ...
Step 2: Identify the common multiples among the two durations:
Common multiples: 210, 420, ...
Step 3: Determine the least common multiple (LCM) by selecting the smallest common multiple from the common multiples:
LCM = 210 minutes.
Now, let's calculate the time when the periods will start together:
The first period of school starts at 8:30 am. Adding 210 minutes to this time:
8:30 am + 3 hours and 30 minutes (210 minutes) = 12:00 pm.
Therefore, the periods for primary classes and other classes will start together at 12:00 pm (noon).
Answer Q7:
To find when the red, green, and yellow lights will flash together again, we need to find the least common multiple (LCM) of the time intervals for each light.
Step 1: Find the LCM of 10 minutes, 12 minutes, and 15 minutes.
To do this, let's list the multiples of each time interval:
Multiples of 10 minutes: 10, 20, 30, 40, 50, 60, 70, ...
Multiples of 12 minutes: 12, 24, 36, 48, 60, 72, ...
Multiples of 15 minutes: 15, 30, 45, 60, 75, ...
Step 2: Identify the common multiples among the three time intervals:
Common multiples: 60, 120, 180, ...
Step 3: Determine the least common multiple (LCM) by selecting the smallest common multiple from the common multiples:
LCM = 60 minutes.
Now, let's calculate the time when the red, green, and yellow lights will flash together again:
The lights flash together at 9:00 pm. Adding 60 minutes to this time:
9:00 pm + 1 hour (60 minutes) = 10:00 pm.
Therefore, the red, green, and yellow lights will flash together again at 10:00 pm.
Answer Q8:
To find when the three bells will ring together again, we need to find the least common multiple (LCM) of the time intervals between the bell rings.
Step 1: Find the LCM of 8 minutes, 15 minutes, and 24 minutes.
To do this, let's list the multiples of each time interval:
Multiples of 8 minutes: 8, 16, 24, 32, 40, 48, 56, ...
Multiples of 15 minutes: 15, 30, 45, 60, 75, ...
Multiples of 24 minutes: 24, 48, 72, ...
Step 2: Identify the common multiples among the three time intervals:
Common multiples: 24, 48, 72, ...
Step 3: Determine the least common multiple (LCM) by selecting the smallest common multiple from the common multiples:
LCM = 24 minutes.
Now, let's calculate the time when the three bells will ring together again:
The bells ring together at 3:00 pm. Adding 24 minutes to this time:
3:00 pm + 24 minutes = 3:24 pm.
Therefore, the three bells will ring together again at 3:24 pm.
Answer Q9:
Let's analyze the cycles of each task:
1. Changing oil: Every 4 months
2. Rotating tires: Every 8 months
3. Replacing air filter: Every 12 months (1 year)
We need to find the least common multiple (LCM) of these three cycles to determine when Mr. Khan will complete all three tasks again.
The LCM of 4, 8, and 12 is 24.
This means that Mr. Khan will complete all three tasks again every 24 months. Since he completed all three tasks in January, the next month he will complete all three tasks again will be January + 24 months = January of the following 2 years.
Therefore, the next month he completes all three tasks will be January of the next 2 years.
Answer Q10:
To find the distance between the fencing posts placed along the sides of the rectangular field, we need to find the greatest common divisor (GCD) of the lengths of the field's sides.
The length of the rectangular field is 300 meters, and the width is 250 meters.
Step 1: Find the GCD of 300 and 250.
Using the prime factorization method:
- 300 = 2^2 * 3 * 5^2
- 250 = 2 * 5^3
Step 2: Identify the common prime factors among 300 and 250.
The common prime factors are 2 and 5.
Step 3: Determine the greatest common divisor (GCD) by selecting the product of the common prime factors with their lowest powers:
GCD = 2 * 5 = 10 meters.
Therefore, the distance between the fencing posts placed along the sides of the rectangular field is 10 meters.
Answer Q11:
To find the highest possible capacity of each bus while accommodating an equal number of students from three classes with 120, 150, and 200 students respectively, we need to determine the greatest common divisor (GCD) of these three numbers.
Step 1: Identify the common factors of 120, 150, and 200:
Factors of 120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Factors of 150: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
Factors of 200: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200
Step 2: Identify the greatest common factor (GCF) from the common factors:
GCF = 10.
Therefore, the highest possible capacity of each bus, while accommodating an equal number of students from the three classes, is 10 students per bus.
Answer Q12:
There are two methods to find LCM of numbers;
- Prime Factorization Method
- Division Method
LCM of 36 and 40 using the Division Method
Therefore, the least common multiple (LCM) of 36 and 40 is 360
Answer Q13:
There are two methods to find HCF of numbers;
- Prime Factorization Method
- Division Method
HCF of 12 and 15 using the Prime Factorization Method
Therefore, the highest common factor (HCF) of 12 and 15 is 3.
HCF of 12 and 15 using the Division Method
Answer Q14:
To find the greatest mass that can be taken an exact number of times from 350g, 510g, and 675g, we need to find the greatest common divisor (GCD) of these three masses.
Step 1: Identify the common factors of 350, 510, and 675:
Factors of 350: 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350
Factors of 510: 1, 2, 3, 5, 6, 10, 15, 17, 30, 34, 51, 85, 102, 170, 255, 510
Factors of 675: 1, 3, 5, 9, 15, 25, 27, 45, 75, 135, 225, 675
Step 2: Identify the greatest common factor (GCF) from the common factors:
GCF = 5.
Therefore, the greatest mass that can be taken an exact number of times from 350g, 510g, and 675g is 5g.
INTEGERS
Ans Q1:
To find how far the rocket engine fell, we need to subtract the depth it reached in the ocean from the altitude it achieved before separation.
Altitude attained by the rocket: 10,400 feet
Depth in the ocean: 1,600 feet
Distance the rocket engine fell = Altitude - Depth
Distance = 10,400 feet - 1,600 feet = 8,800 feet.
Therefore, the rocket engine fell a distance of 8,800 feet.
Ans Q2:
Ahmed's score after two rounds can be calculated by adding his gains and losses from each round.
In the first round, he lost 29 points.
In the second round, he gained 34 points.
His total score after two rounds = Loss in the first round + Gain in the second round
Total score = (-29) + 34 = 5 points.
Therefore, Ahmed's score after two rounds is 5 points.
Ans Q3:
To find the boiling point of copper, we need to add the temperature difference (1,479°C) to its melting point (1,083°C).
Boiling point = Melting point + Temperature difference
Boiling point = 1,083°C + 1,479°C = 2,562°C.
Therefore, the boiling point of copper is 2,562°C.
Ans Q4:
The submarine's new altitude can be found by adding the change in altitude (diving down 1600 feet) to its initial altitude.
Initial altitude = -5600 feet
Change in altitude = +1600 feet (diving down)
New altitude = Initial altitude + Change in altitude
New altitude = -5600 feet + 1600 feet = -4000 feet.
Therefore, the submarine's new altitude is -4000 feet.
Ans Q5:
To calculate Ali's score after three rounds, we need to sum up his gains and losses from each round.
In the first round, he gained 28 points.
In the second round, he gained 20 points.
In the third round, he lost 35 points.
His total score after three rounds = Gain in the first round + Gain in the second round - Loss in the third round
Total score = 28 + 20 - 35 = 13 points.
Therefore, Ali's score after three rounds is 13 points.
Ans Q6:
To find the total change in the value of Mr. Fahad's shares of stock for Monday, we need to multiply the change in the price of each share by the number of shares he owns.
Change in price per share = Rs. 8
Number of shares owned = 28
Total change in value = Change in price per share * Number of shares owned
Total change in value = 8 * 28 = Rs. 224.
Therefore, the total change in the value of Mr. Fahad's shares of stock for Monday is Rs. 224.
Ans Q7:
To find the temperature at 6pm, we'll start with the initial temperature at noon and then account for the changes that occurred.
Initial temperature at noon = 39°F
Temperature dropped by 5°F and then rose by 4°F
Temperature change = (-5°F) + 4°F = -1°F.
Now, we'll subtract the temperature change from the initial temperature to find the temperature at 6pm:
Temperature at 6pm = Initial temperature at noon + Temperature change
Temperature at 6pm = 39°F - 1°F = 38°F.
Therefore, the temperature at 6pm was 38°F.



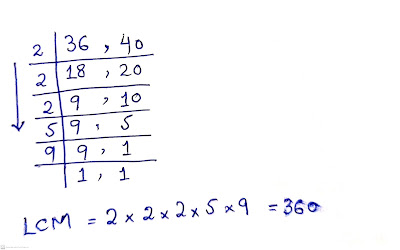



Comments
Post a Comment